prim 알고리즘

신장트리란?

신장트리란 연결 그래프의 부분 그래프이다. 그래프는 속도는 높지만 사이클이 존재하므로 비용이 많이 들게 된다. 신장트리는 사이클이 존재해서는 안되므로 속도측면에서는 그래프보다 뒤떨어질 수 있어도 비용 측면에서 그래프보다 우세하다. 정리해보면 신장트리에서 모든 노드는 적어도 하나의 간선에 연결되어 있어야 하며 그 대신에 사이클이 형성되면 안된다.

최소 비용 신장 트리란?

그래프의 간선에 가중치가 부여된 그래프를 가중치 그래프 또는 네트워크라고 한다.

이때 가중치란 비용이나 거리를 의미하는 값이 될 수 있다. 가중치가 부여된 무방향 그래프의 신장 트리 비용은 신장트리를 구성하는 모든 간선의 비용을 합한 것이다.

여기서 말하는 최소 비용 신장트리는 트리를 구성하는 간선들의 가중치를 합한 것이 최소가 되는 신장 트리이다.

dfs 나 bfs 로 쉽게 구현할 수 있는 그냥 신장트리와는 다르다.

이러한 최소 비용 신장 트리는 도로 건설 (도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제) , 통신 (전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제), 배관 (파이프의 총 길이가 최소가 되도록 연결하는 문제) 등에 사용 된다.

탐욕적 알고리즘

탐욕적 알고리즘은 동적 프로그래밍과 정반대의 전략이다. 큰 문제를 작은 문제로 나누어 엄격한 계획하에 '재귀적 속성'을 찾아서 최종적인 해답을 찾아내는 동적 프로그램과 반대로 탐욕적 알고리즘은 매순간 선택의 과정을 거치는데 그 선택은 국부적이다. 작은 문제의 결과 값이 항상 같다는 보장을 이용해 큰 문제를 해결해 나가는 동적 프로그램과는 다르게 탐욕적 알고리즘은 최적이라고 생각했던 작은 부분들을 모아서 최종적인 해답을 만들었다고 해서, 그 해답이 궁극적으로 최적이라는 보장이 없다. 따라서 탐욕적인 알고리즘은 항상 최적의 해답을 주는지 반드시 검증해야 한다. (Greedy 알고리즘은 항상 최선이 아니기 때문에 이에 대한 검증이 필요하다는 것으로 이해해도 될 것 같다.)

 

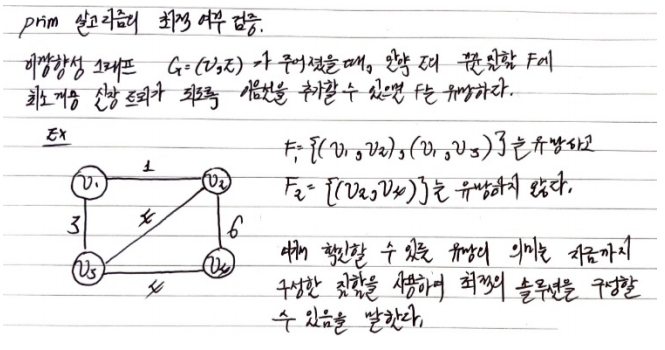
따라서 정리해보면 Prim 의 알고리즘에서 구성되는 각 단계의 F 들이 유망함을 보이면 최적임을 보일 수 있다는 것이다.

이번 토론 내용은 Greedy 알고리즘 중 Prims 알고리즘의 아이디어에 대해 기술하는 것이다.

Prims

Greedy 방법에 속하지만 최적화를 보장하는 알고리즘이다.

Prim 알고리즘이란 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법인데 Prim 알고리즘의 동작에 대해 알아보면

1. 시작 단계에서는 시작 정점만이 MST (최소 비용 신장 트리) 집합에 포함된다.
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다. (가중치가 가장 낮은 것을 먼저 선택한다.)
   • 선정 절차 / 적정성 점검 : Y 에 속한 임의의 정점과 가장 가까운(즉 가중치가 가장 낮은) V - Y 에 속한 정점 하나를 선정한다. ( V - Y 와 Y 의 함수이므로 자연스럽게 순환은 생기지 않는다)
   • 두 정점을 연결하는 이음선을 F 에 추가한다.
   • 선정한 정점을 Y에 추가한다.
   • Y = V 가 되면(즉 모든 Vertex 를 다 순회하면), T = (V, F) 가 최소 비용 신장 트리이다.
   (연결된 간선과 연결되지 않은 간선 중 가중치가 최소인 간선을 계속해서 연결해준다.)
3. 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.

그림으로... 보면...

(좀 못생겼지만...)

 

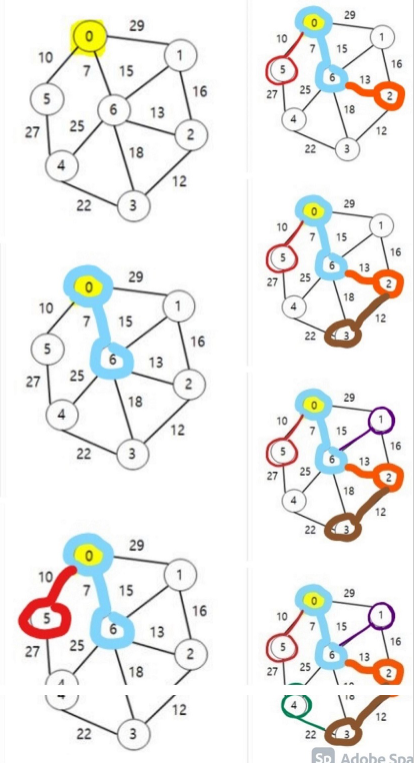
소스코드

• prim

#include <stdio.h>
#include <stdbool.h>

#define INF 987654
#define Vertex 7

#define Min(x, y) ((x) < (y) ? (x) : (y))

int weight[Vertex][Vertex] = {
    {0 ,   29,  INF,   INF,  INF,   10,    7},
    {29 ,   0,   16,   INF,  INF,  INF,   15},
    {INF,  16,    0,    12,  INF,  INF,   13},
    {INF,  INF,  12,     0,   22,  INF,   18},
    {INF,  INF,  INF,   22,    0,   27,   25},
    {10 ,  INF,  INF,  INF,   27,    0,  INF},
    {7  ,  15,    13,   18,   25,  INF,    0}
};

int distance[Vertex];
// 시작 정점으로 부터의 최단 거리

int visited[Vertex];

int MinVertex() {
    int v, i;
    for (i = 0; i < Vertex; i++) {
        if (!visited[i]) {
            v = i;
            break;
        }
    }
    for (i = 0; i < Vertex; i++) {
        if (!visited[i] && (distance[i] < distance[v])) {
            // 가중치를 바탕으로 정렬된 가장 작은 distance 를 계속 돌려줄 것이다.
            // 여기서 방문된 것들을 제외한 distance의 인덱스를 돌려주면 그게 정점이된다.
            v = i;
        }
    }
    return v;
}

void prim(int start_v) {
    int u, v;

    // 초기화 부분이다.
    for (u = 0; u < Vertex; u++) {
        distance[u] = INF;
        visited[u] = false;
    }

    // 맨처음 distance 에는 자기 자신을 가리키는 가중치 0이 들어간다.
    distance[start_v] = 0;

    for (int i = 0; i < Vertex; i++) {
        u = MinVertex();
        visited[u] = true; 

        if (distance[u] == INF)
            return;

        printf("%d\n", u);

        for (v = 0; v < Vertex; v++) {
            if ((weight[u][v] != INF) && (!visited[v]) && (weight[u][v] < distance[v])) {
                // 연결되었으며 방문한 적이 없고 현재 연결된 간선들 중에서 가중치가 제일 작은 것을 고르는 부분이다.
                distance[v] = weight[u][v];
                // 가중치를 distance 에 작은 순서대로 넣어줄 수 있다.
            }
        }
    }
}

int main(void) {
    prim(0);
}

int MinVertex() {
    int v, i;
    for (i = 0; i < Vertex; i++) {
        if (!visited[i]) {
            v = i;
            break;
        }
    }
    for (i = 0; i < Vertex; i++) {
        if (!visited[i] && (distance[i] < distance[v])) {
            // 가중치를 바탕으로 정렬된 가장 작은 distance 를 계속 돌려줄 것이다.
            // 여기서 방문된 것들을 제외한 distance의 인덱스를 돌려주면 그게 정점이된다.
            v = i;
        }
    }
    return v;
}

• 시간 복잡도

Graph 의 정점의 개수가 n 개라고 했을 때 이를 인접행렬로 구현한 경우

결구 n X n 을 다 탐색해 보아야 하므로 O(nxn) 이 된다.